多项式曲线与结果不符

Question

我遇到了我的阻力极曲线拟合中CD值过大的问题。以下是我的升力系数和阻力系数的值：

升力系数如下：

[-0.2863876, -0.15198764, -0.00709039, 0.1414652, 0.28727075, 0.43092027,
 0.57339435, 0.71901446, 0.95383017, 1.00155515, 1.04740696, 0.93310272]

阻力系数如下：

[-0.02768897, -0.03168675, -0.03116817, -0.02166403, -0.00677296, 0.01566423,
 0.04477065, 0.08153319, 0.16150749, 0.19508941, 0.21802003, 0.12811101]

我使用的代码如下：

def test_func(CL, k, CD_0):
    return k*(CL**2) + CD_0  # 阻力极函数

popt, pcov = curve_fit(test_func, CD, CL, p0=[1, 0.01])

k_opt, CD_0_opt = popt 

CL_model = np.linspace(min(CL), max(CL), 100)
CD_model = test_func(CL_model, k_opt, CD_0_opt)

我尝试调整了初始猜测值p0，但这对曲线拟合没有产生影响。

hsz · Answer

您已经非常接近了，但似乎您将"x"和"y"的概念在脑中混淆了。观察您提供的图表，您怎么能期望这样的数据通过曲线拟合呢？因为根据这个图，对于单一的$C_D$值，存在多个可能的$C_L$值，这违反了函数映射的基本原则。

从您的函数来看，它似乎是根据$C_L$值预测$C_D$值的，因此在这种情况下，"x"应该是升力系数($C_L$)，而"y"是阻力系数($C_D$)。如果将两者的位置互换，并使用curve_fit函数，按照正确的变量顺序进行操作，问题就能得到解决。我使用您提供的系数数据进行了尝试，代码和生成的图表如下所示：

# 复制您提供的数据，但请注意，您最后两个数据点有些异常（可能是误差较大的离群点，或者数据输入有误，也可能是顺序颠倒了）
CL = np.array([-0.2863876, -0.15198764, -0.00709039, 0.1414652, 0.28727075, 0.43092027, 
              0.57339435, 0.71901446, 0.95383017, 1.00155515, 1.04740696, 0.93310272])
CD = np.array([-0.02768897, -0.03168675, -0.03116817, -0.02166403, -0.00677296, 0.01566423, 
              0.04477065, 0.08153319, 0.16150749, 0.19508941, 0.21802003, 0.12811101])

def test_func(CL, k, CD_0):
    return k*(CL**2) + CD_0  # 您的测试函数，根据CL(x)预测CD(y)

popt, pcov = curve_fit(test_func, CL, CD, p0=[1., 0.01])  # 注意这里CL作为第一个参数，因为它是我们关注的"x"变量，CD作为拟合目标"y"

# 绘制结果
plt.scatter(CL, CD, marker="x", label="数据", c="dodgerblue")
CL_model = np.linspace(np.min(CL), np.max(CL), 100)
CD_model = test_func(CL_model, *popt)
plt.plot(CL_model, CD_model, label=rf"模型: k = {popt[0]:.2f}, $CD_0$ = {popt[1]:.2f}", c="orange")
plt.legend()
plt.xlabel(r"$C_L$")
plt.ylabel(r"$C_D$")
plt.show()

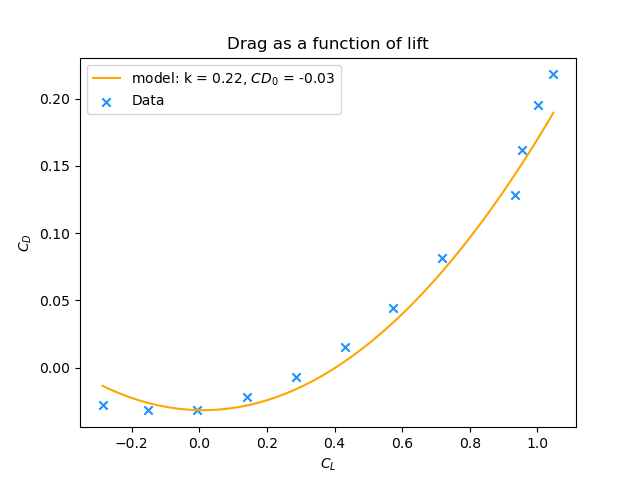
plot_image

但是，正如@JJacquelin在其回答中指出的那样，您可能需要考虑更改用于拟合数据的函数形式。选择形如$y = x² + c$的函数意味着曲线的最小值必须正好位于$x = 0$处，然而您的数据显示情况并非如此。同时，您应当检查数据，并剔除任何不符合此类模型物理合理性的数据点。

Laurenz Albe · Answer

考虑到变量$x$代表升力系数，而$y$代表阻力系数，我们注意到$y(x)$的最小值并不恰好位于$x=0$这一点。

因此，相较于模型$y(x)=Ax²+C$，采用模型$y(x)=ax²+b*x+c$会更为合适，因为这样可以捕捉到$x$轴上的偏移，即最小值不位于原点的情况。

二次回归图像

备注：在进行二次回归分析时，未将最后一个数据点（$x=0.93310272$，$y=0.12811101$）纳入考量。这是因为该点接近曲线上拐点的位置，将其纳入可能会对拟合效果产生不必要的干扰。